What is chaos? We hear the term often enough, what does it mean? There are many aspects of our universe that seem to have no order, make no sense and have no underlying structure. They just ‘are’, and will continue to ‘be’. This is satisfactory for some, but others struggle to accept that some things are just too chaotic for us to ever understand. These same people may also believe that there must be some underlying structure to these systems, that there cannot just be total chaos. Chaos theory is the process of trying to discover the structures and processes that are present within these systems and to understand and predict future outcomes. At this stage it may be useful to mention a few systems that are chaotic in their structure. There are changes in the weather, the movement of satellites in the solar system, ecology and population growth, molecular vibrations. There is also speculation over the existence of chaotic dynamics in plate tectonics and in economics. Ecology still remains one of the best examples of a chaotic system. Population growth and distribution, like all chaotic systems, are very dynamic and deterministic, meaning that future outcomes depend heavily on initial conditions. This is the basis of chaos theory: the hope that we can understand the structure and differences caused in various outcomes through differences in the systems initial input.
A fine example of another chaotic system is the markings on animals. We identify different species by their distinct markings and colourings. At a glance the markings within one species seem to be identical, but closer inspection reveals that there are differences between each animals markings. These markings tend to follow a set of basic parameters, but allow for a certain amount of deviation from these parameters. These deviations are what allow animals to recognise each other and be unique, though still look similar to others within their species. Chaos theorists aim to understand the factors that cause these deviations and to understand future outcomes of the system through understanding those deviations and their causes.
The first real experimenter in the field of chaos was Edward Lorenz, an American meteorologist. Lorenz was studying weather patterns. He had a set of twelve equations which he used to model what the weather may be. During one day of study in 1961, Lorenz wanted to look at a particular set of results again. Rather than run the test from the beginning, he decided to start it off half way through in order to save some time. He entered a number that he had gained from his previous run through of the experiment, one from half-way through the results. This was his initial value. After leaving the equations to run for some time, he returned to observe the results. What he discovered was that the set of results he had ended up with this time differed greatly from those found after the first run of tests. His computer had stored 6 digits of data in its memory, though to save paper Lorenz had only printed out the data to 3 decimal places. When Lorenz went to enter the data for the second run of tests he only entered the first 3 decimal places. In the original sequence, the number was .506127, and he had only typed the first three digits, .506. This is what had led to the vastly different outcome to the experiment, despite the fact that the difference in the input number was tiny. This came to be known as the Butterfly Effect.
“The flapping of a single butterfly’s wing today produces a tiny change in the state of the atmosphere. Over a period of time, what the atmosphere actually does diverges from what it would have done. So, in a month’s time, a tornado that would have devastated the Indonesian coast doesn’t happen. Or maybe one that wasn’t going to happen, does.” – Ian Stewart, Does God Play Dice? The Mathematics of Chaos
It became apparent to Lorenz that all that was needed to dramatically alter the outcome of an experiment was a tiny amount of variation the initial values. This degree of difference could be the result of a number of factors, such as background noise, electrical interference or an inaccuracy with the equipment being used. For example, an experiment with an initial value of 8 could produce a vastly different outcome if the input value became 8.000001. This is a level of accuracy which we would struggle to keep up with, therefore the greatly differing outcomes of experiments using these inputs would also be incredibly difficult to understand and apply logic to.
This is exactly the problem Lorenz found himself facing. he realised that in order to understand the phenomenon better he needed to simplify the computations, whilst still making sure they remained sensitive to initial conditions. He stripped down equations used to calculate convection to the point where they no longer had anything to do with convection as a result of their exaggerated simplicity, but still retained the sensitivity to initial conditions that he required. His equations described a water wheel.
“At the top, water drips steadily into containers hanging on the wheel’s rim. Each container drips steadily from a small hole. If the stream of water is slow, the top containers never fill fast enough to overcome friction, but if the stream is faster, the weight starts to turn the wheel. The rotation might become continuous. Or if the stream is so fast that the heavy containers swing all the way around the bottom and up the other side, the wheel might then slow, stop, and reverse its rotation, turning first one way and then the other.” – James Gleick, Chaos – Making a New Science
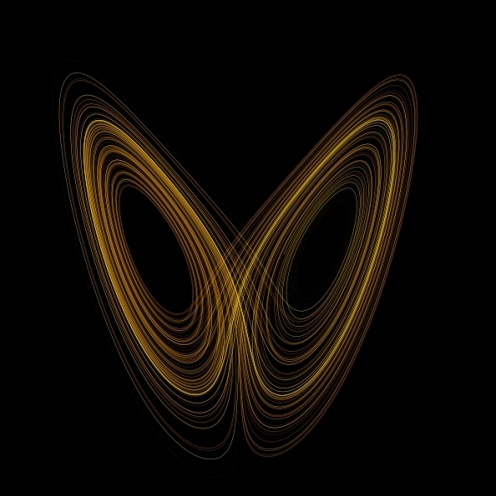
The experiment looked as though it produced random results, through when graphed these results did not look random at all.
“There were only two kinds of order previously known: a steady state, in which the variables never change, and periodic behavior, in which the system goes into a loop, repeating itself indefinitely. Lorenz’s equations were definitely ordered – they always followed a spiral. They never settled down to a single point, but since they never repeated the same thing, they weren’t periodic either. He called the image he got when he graphed the equations the Lorenz attractor.” – In My Humble Opinion
In 1963, Lorenz went about publishing his findings in a journal, though unfortunately he was only able to publish in a meteorological journal on account of him being a meteorologist. This resulted in his findings being ignored by physicists and mathematicians, the very people who would be most interested in his findings. This meant that although Lorenz had discovered something revolutionary, he had to wait for someone to discover it and come to him.
There is plenty more to talk about on this topic, but that is for another day. I will leave you with this much for now and post Chaos Theory – Part Two soon.

Leave a Comment